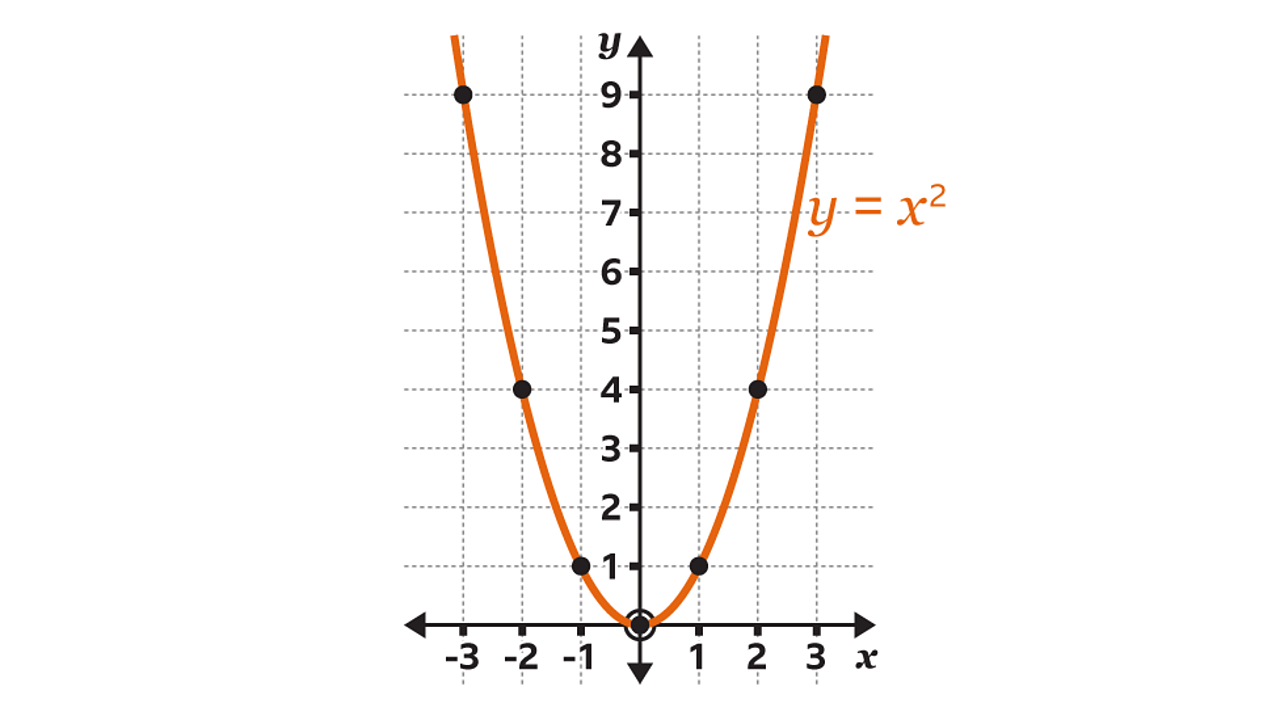
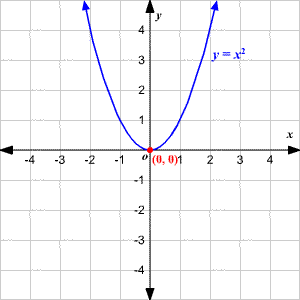
√無料でダウンロード! y=x^2 1 290967-Y=x^2+1 graph
Graph y2=2 (x1) y − 2 = −2(x − 1) y 2 = 2 ( x 1) Move all terms not containing y y to the right side of the equation Tap for more steps y = −2x4 y = 2 x 4 Use the slopeintercept form
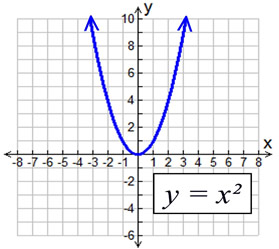
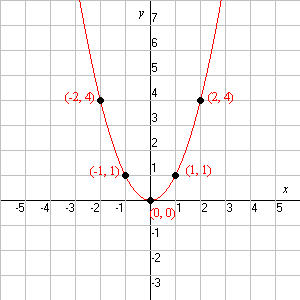
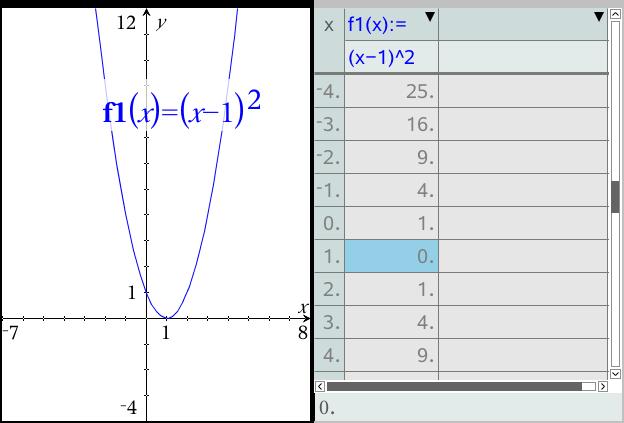
Y=x^2+1 graph-Algebra Graph y= (x1)^2 y = (x − 1)2 y = ( x 1) 2 Find the properties of the given parabola Tap for more steps Direction Opens Up Vertex (1,0) ( 1, 0) Focus (1, 1 4) ( 1, 1 4) Axis ofGraph y=x^22x1 y = x2 2x − 1 y = x 2 2 x 1 Find the properties of the given parabola Tap for more steps Direction Opens Up Vertex (−1,−2) ( 1, 2) Focus (−1,−7 4) ( 1, 7 4) Axis
Y=x^2+1 graphのギャラリー
各画像をクリックすると、ダウンロードまたは拡大表示できます
 | ||
 |  |  |
 |  |  |
 |  | |
「Y=x^2+1 graph」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  | |
 |  | |
 |  |  |
「Y=x^2+1 graph」の画像ギャラリー、詳細は各画像をクリックしてください。
 | ||
 | 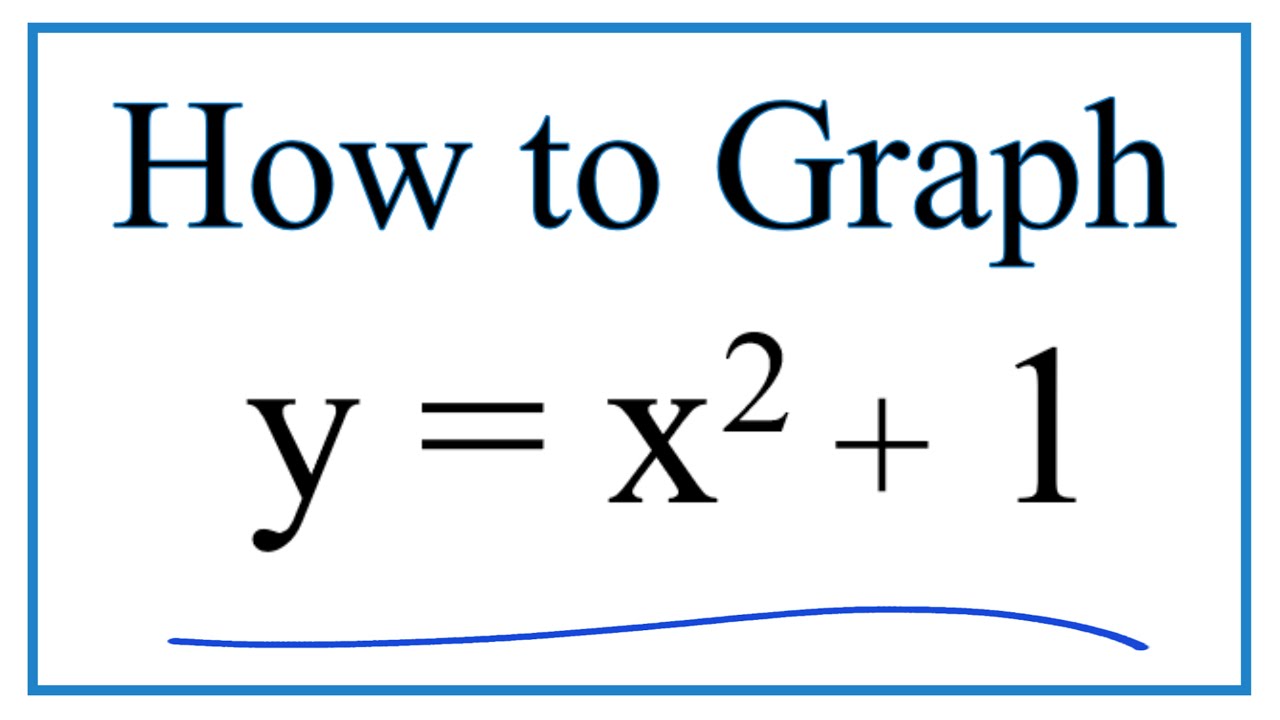 | |
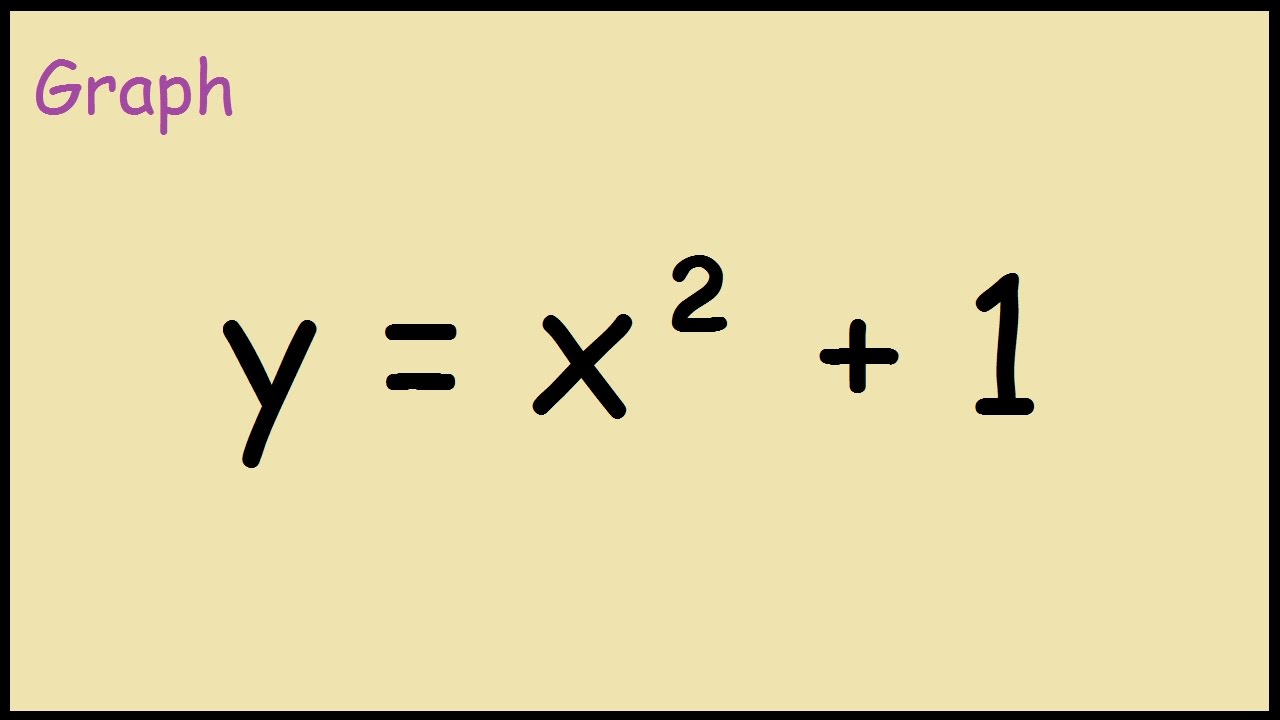 |  | |
 |  | |
「Y=x^2+1 graph」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 | ||
 |  |  |
 |  | |
「Y=x^2+1 graph」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 | ||
 | ||
「Y=x^2+1 graph」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 | ||
 | ||
 |  |  |
「Y=x^2+1 graph」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  | |
 |  |  |
 |  |  |
「Y=x^2+1 graph」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 |  |  |
 |  | |
「Y=x^2+1 graph」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 | 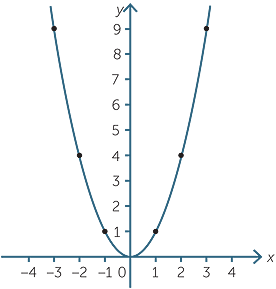 | 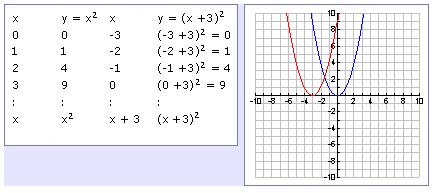 |
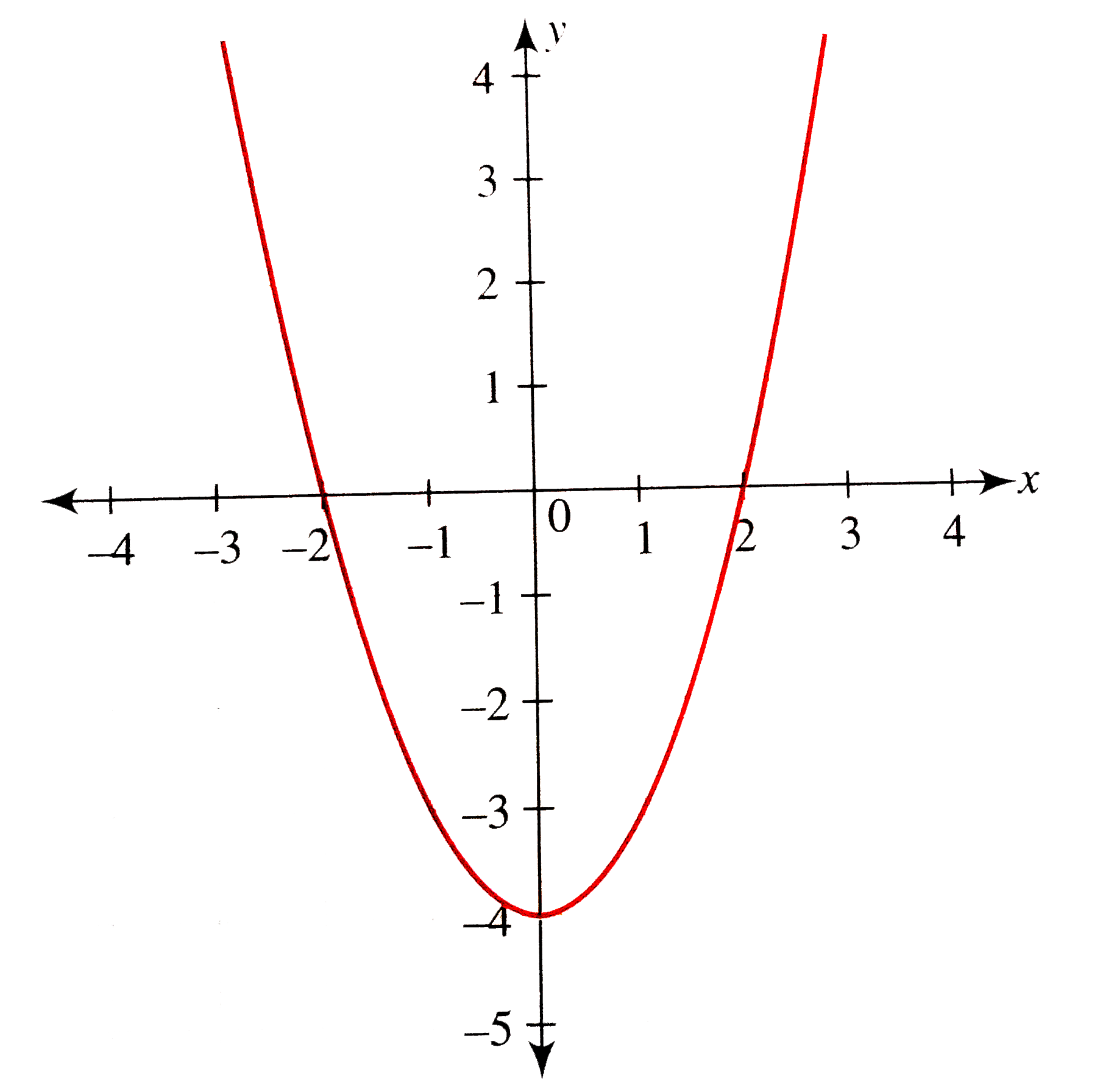
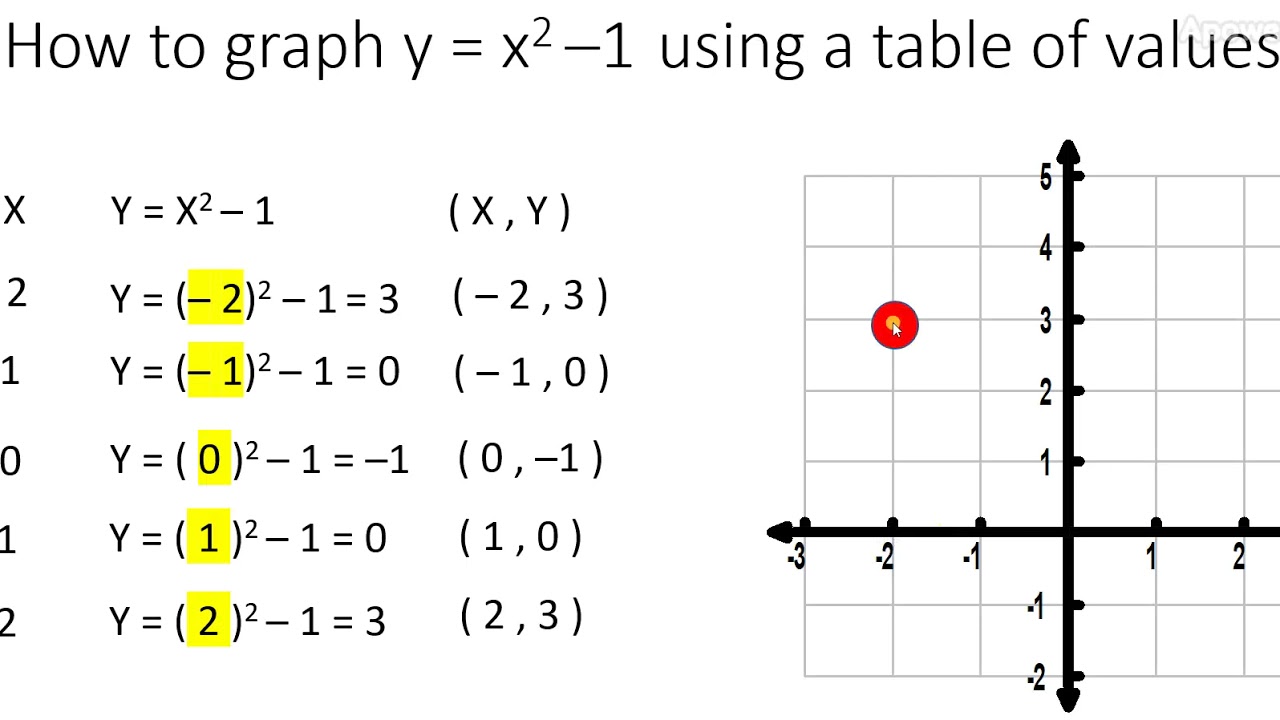
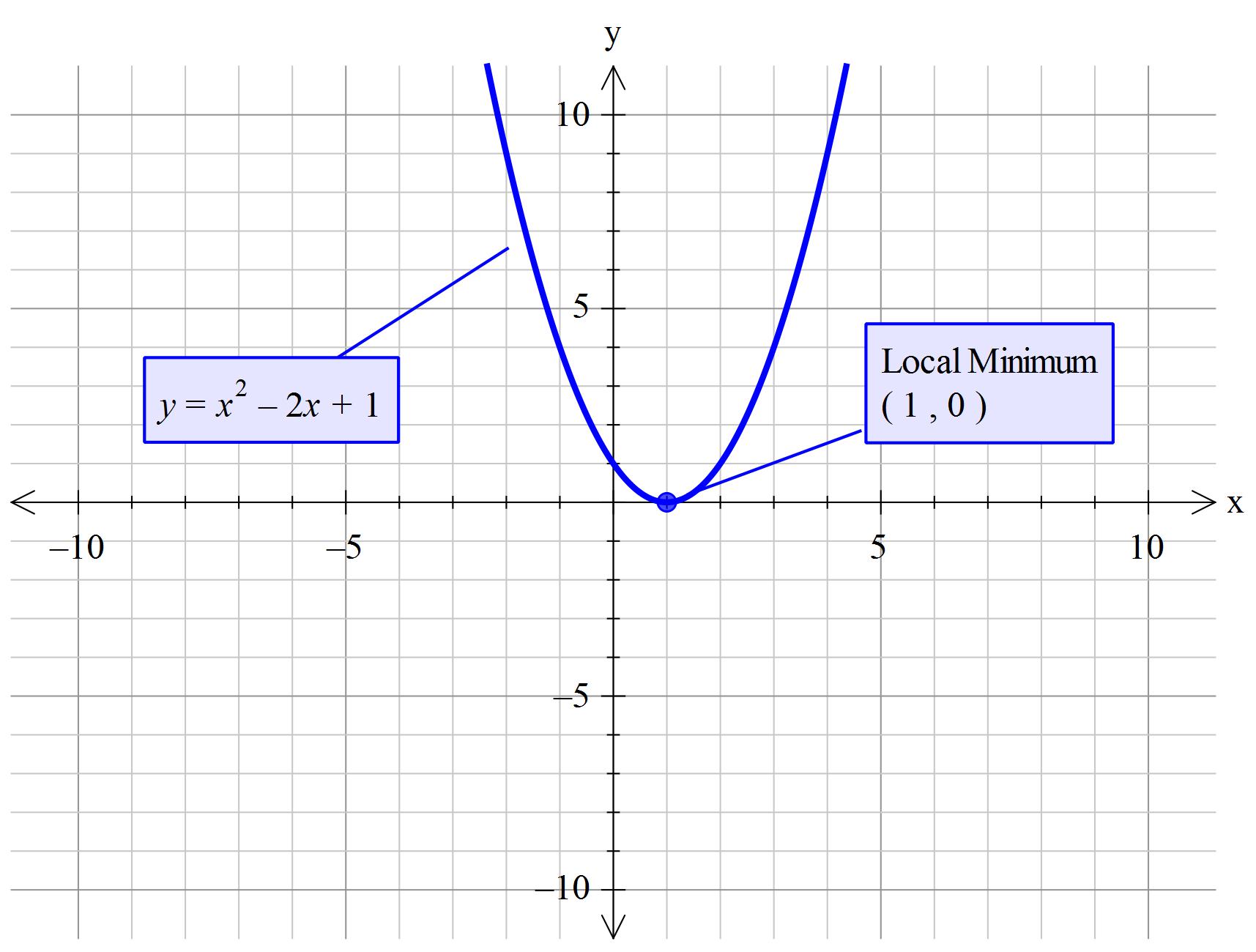
Graph y=x^21 y = x2 − 1 y = x 2 1 Find the properties of the given parabola Tap for more steps Direction Opens Up Vertex (0,−1) ( 0, 1) Focus (0,−3 4) ( 0, 3 4) Axis of Symmetry x = 0 x =Y = (x − 2)2 − 1 y = ( x 2) 2 1 Find the properties of the given parabola Tap for more steps Direction Opens Up Vertex (2,−1) ( 2, 1) Focus (2,−3 4) ( 2, 3 4) Axis of Symmetry x = 2 x =
Incoming Term: x 2 10x 24 axis of symmetry, y=x^2+1, y=x^2+1 graph, y=x^2-16, y=x^2-10, y=(x^2+1)^3, y=x^2-100, y''(x^2+1)=2xy', y=x^2-12, y=(x^2-1)^m,
コメント
コメントを投稿