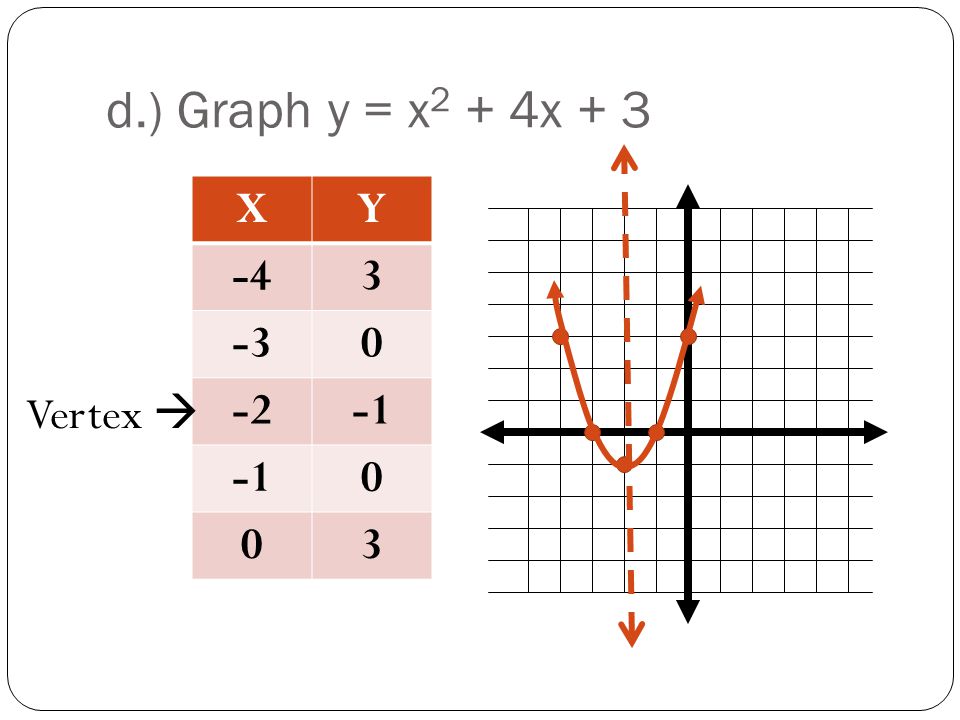
画像 y=x^2-4x 3 vertex 201504

Consider y = x² which has its vertex at (0, 0) y = (x 6)² is a translation 6 units to the left so the vertex moves to (6, 0) y = 3(x 6)² is a stretch (squeeze) parallel to the x axis which does not affect points on the x axis so the vertex stays at (6, 0)Vertex\(y3)^2=8(x5) vertex\(x3)^2=(y1) parabolavertexcalculator vertex y=2x^{2}4x12 en Related Symbolab blog posts Practice, practice, practice Math can be an intimidating subject Each new topic we learn has symbols and problems we have never seen The unknowingFind the Vertex Form y=x^23 Complete the square for Tap for more steps Use the form , to find the values of , , and Consider the vertex form of a parabola Substitute the values of and into the formula Cancel the common factor of and Tap for more steps Factor out of

Given Function F X X2 4x 5 Determine The Vertex Axis Of Symmetry Calculate Y Intercept Find Additional Point On Graph Graph Function Submit Graph Enotes Com

Y=x^2-4x 3 vertex

Y=x^2-4x 3 vertex- Write the quadratic function given in vertex forms y= 3(x2) ^2 5 in standard form asked in ALGEBRA 2 by anonymous standardformofanequationWrite an equation in vertex form m = a (x – h)^2 K Now, expand the square formula m = a (x^2 y^2 2hx) K Multiply the inner side or bracket a x^2 a y^2 2

Quadratic Function

Get stepbystep solutions from expert tutors as fast as 1530 minutes Your first 5 questions are on us!Hi the vertex form of a parabola, where(h,k) is the vertexY=x^24x3 in vertex form Y=x^24x3 in vertex form How to solve for vertex form y = x^2 4x – 1 Answers 2 Get Other questions on the subject Mathematics Mathematics, 1330, mbatton879 In the coordinate plan (6,9) b (3,9) c (3,3) def is shown in the coordinate plan below Answers 1 continue Rewrite in \(y=a(x−h)^{2}k\) form and determine the

 View Chapter 2 Project Pre Calculusdocx from MAC 1140 at Florida International University Yousef El Hajj Chapter 2 Project 1 identify the vertex and intercepts of the graph of y=x^24x3 A) TheA free online vertex form calculator can convert vertex form to the standard form of a parabola If you want to know how to change the vertex to standard form, let's start!The Distance Between The Vertex Of The Parabola Y X 2 4x 3 And The Centre Of The Circle The distance between the vertex of the parabola y = x 2 4x 3 and the centre of the circle x 2 = 9 (y 3) 2 is 1) 2√3 units 2) 3√2 units 3) 2√2 units 4) √2 units 5) 2√5 units

 Complete the square to write y = 3x2 12x 7 in vertex form, y = a(x h)2 k y = 3(x2 4x) 7 y = 3(x2 4x 4) 7 Vertex is (2,4) Step 1 Complete the square y = − x2 − 4x = −(x − 2)2 −4 Step 2 Arrange so that you get the form (x −xv)2 = 4a(y − yv) y = − (x −2)2 −4 = −(x −2)2 4 ⇒ (x − 2)2 = 4 − y ⇒ (x − 2)2 = −(y − 4) From here you can conclude that the vertex is at (2 `y=2(0)^24(0)3=3` So the yintercept is (0,3) To find the xintercepts, you plug in y=0 and solve for x This is a little harder `0=2x^24x3` There are two ways to solve something like this

Parabolas

How Do You Find The Vertex Of Y 2x 2 4x Socratic

Get an answer for 'graph y=3/4x^2 plot the vertex and four additional points, two on each side of the vertex' and find homework help for other Math questions at eNotesGiven {eq}y = 2x^2 4x 3 {/eq}; vertex = (1, 1 ) Stepbystep explanation Given the equation of a parabola in standard form f(x) = ax² bx c ( a ≠ 0 ) Then the x coordinate of the vertex is x = f(x) = 2x² 4x 3 ← is in standard form with a = 2 and b = 4 , then = = 1 Substitute x = 1 into f(x) for corresponding y coordinate of vertex

Solved Q X 2x 2 4x 3 A Write In Vertex Form B Chegg Com

Orcca Completing The Square

All equations of the form a x 2 b x c = 0 can be solved using the quadratic formula 2 a − b ± b 2 − 4 a c The quadratic formula gives two solutions, one when ± is addition and one when it is subtraction x^ {2}4xy5=0 x 2 4 x − y − 5 = 0 This equation is in standard form ax^ {2}bxc=0 Substitute 1 for a, 4 for b, andFind the Vertex y=2x^24x3 y = 2x2 − 4x − 3 y = 2 x 2 4 x 3 Rewrite the equation in vertex form Tap for more steps Complete the square for 2 x 2 − 4 x − 3 2 x 2 4 x 3 Tap for more steps Use the form a x 2 b x c a x 2 b x c, to find the values of a a, b b, and c c a = 2, b = − 4, c = − 3 a = 2, b = 4, cGiven a parabola whose equation is {eq}y=x^24x3 {/eq} Then we have that {eq}a=1, b=4, c=3 {/eq} To graph the parabola we first have to find its characteristic points

Determine Which Of The Following Statements Is True Concerning The Values Described In Column 1 And Column 2 Column 1 Column

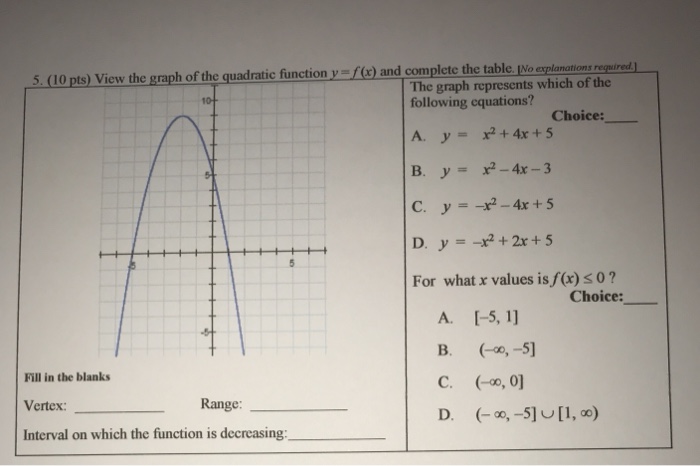
Solved 0 Pts View The Graph Of The Quadratic Function Y F Chegg Com

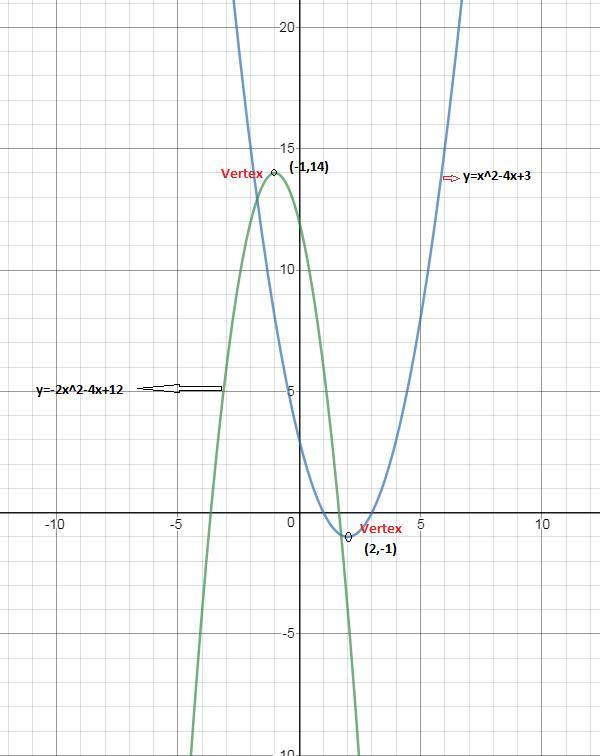
Algebra Graph y=2x^24x3 y = 2x2 4x − 3 y = 2 x 2 4 x 3 Find the properties of the given parabola Tap for more steps Rewrite the equation in vertex form Tap for more steps Complete the square for 2 x 2 4 x − 3 2 x 2 4 x 3 To find corresponding value of ycoord of vertex , substitute x = 2 into the function x = 2 y = −(2)2 4(2) −3 = − 4 8 − 3 = 1 ⇒ vertex = ∣∣ ∣ ∣¯¯¯¯¯¯¯¯¯¯¯¯¯¯a a 2,1 a a ∣∣ −−−−−−− − Here is the graph of y#= x^24x3 graph {x^24x3 10, 10, 5, 5} Answer linkGiven the equation y = 3x^2 x 3 To find the vertex of a parabola 1 Establish the values for a, b, and c in the given equation a = 3, b = 1, c = 3

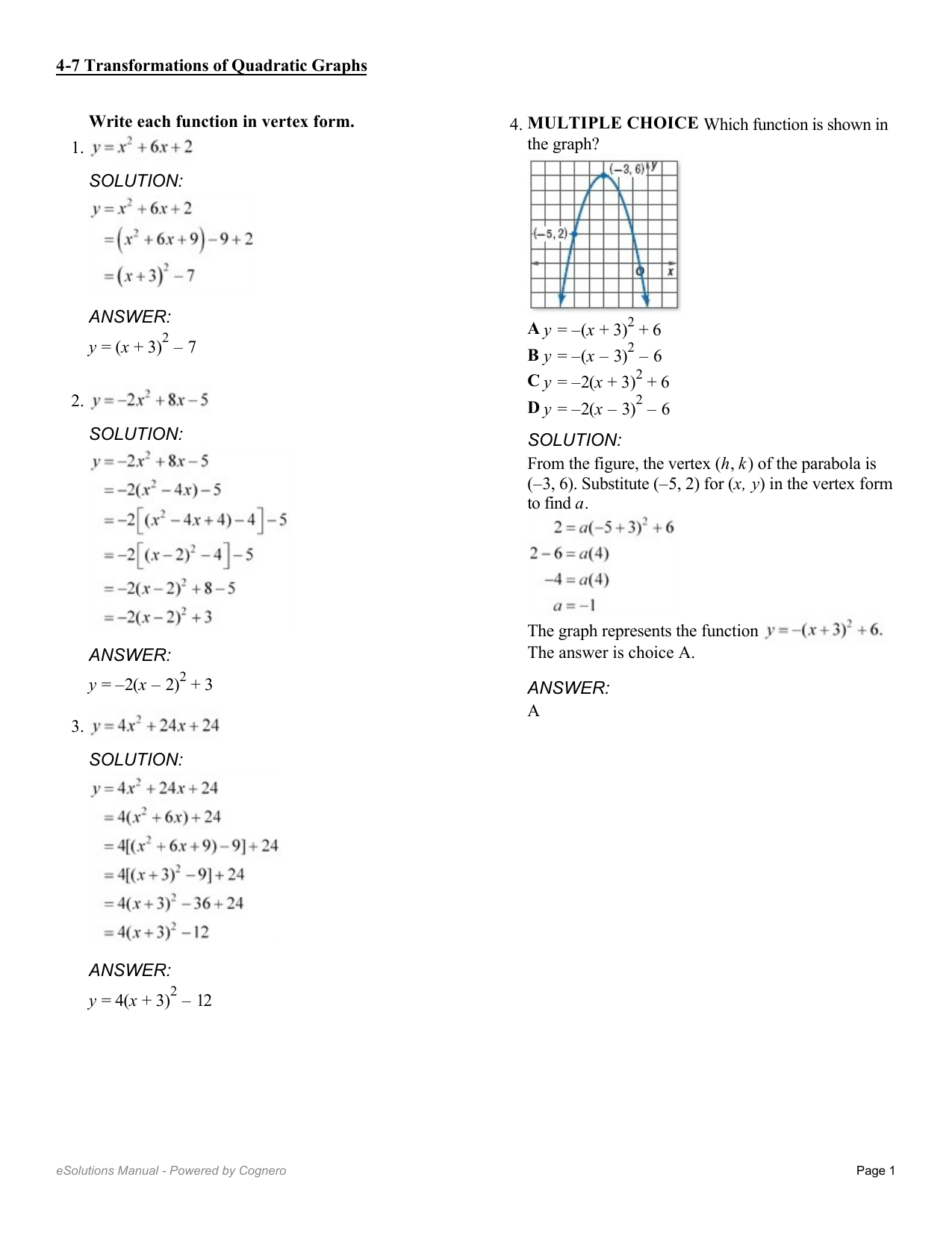
Write Each Function In Vertex Form 1 Solution Answer Y X

Pcc Instructure Com

🔴 Answer 2 🔴 on a question 3 Write y = x2 4x 6 in vertex form A y = (x 2)2 2 B y = (x 2)2 2 C y = (x 2)2 4 D y = (x 2)2 4 the answers to ihomeworkhelperscomAnswer (1 of 3) There's no need to use graping software not that there's anything wrong with that, except that it doesn't really give any insight you can complete the square notice that y^2 2y is very similar to y^2 2y 1 = (y1)^2 So y^2 2y = (y1)^2 1 which means y^2 4xThe vertex is at (p,q)=(2,1) You can find the y=intercept by setting x=0 and solving for y It's easiest to do this with the general form y=x^24x3 y = 0)3 y=3 The yintercept is y=3 To find the xintercepts, factor, set y=0 and solve for x You have to solve by factoring y=x^24x3 0 = x^24x3 0 = (x3)(x1) Which means that the x

Quadratic Functions

2 02 Quadratic Equations

 Answer y = x² 4x 12 When y = 0 x² 4x 12 = 0 x² 4x 12 = 0 (x 2)(x 6) = 0 x = 2 or x = 6 The xintercepts are 2 and 6 y = (x² 4x) 12 yCorrect answer to the question 3 Write y = x2 4x 6 in vertex form A y = (x 2)2 2 B y = (x 2)2 2 C y = (x 2)2 4 D y = (x 2)2 4Find the Vertex Form y=x^24x3 Complete the square for Tap for more steps Use the form , to find the values of , , and Consider the vertex form of a parabola Substitute the values of and into the formula Simplify the right side Tap for more steps Cancel the common factor of and

Solving Quadratic Equations By Graphing Ppt Video Online Download

Graphing Quadratic Functions

Given the parabola with standard equation {eq}y=\dfrac{3}{4}x^2 {/eq} Then we have that {eq}h=k=0, a=\dfrac{3}{4} {/eq}, so the vertex is the point {eq}V(0,0) {/eq}Answers The general equation of a quadratic is expressed as y = ax^2bxc To convert the general equation to vertex form, we need to obtain this form (y k)= a (x h)^2 This could be done by using completing the square method y = –3x^2 – 12x – 2 y 2 = –3 (x^2 4x)Janine da Silva The graph of the quadratic function f (x) = 3 4 x – x 2 intersects the yaxis at point A and has its vertex at point B (a) Find the coordinates of B (3 A quadratic function, f (x) = ax 2 bx, is represented by the mapping diagram below

1st Semester Algebra 2 Exam Review Graphing Functions Flashcards Quizlet

How To Find The Vertex Of A Quadratic Equation 10 Steps

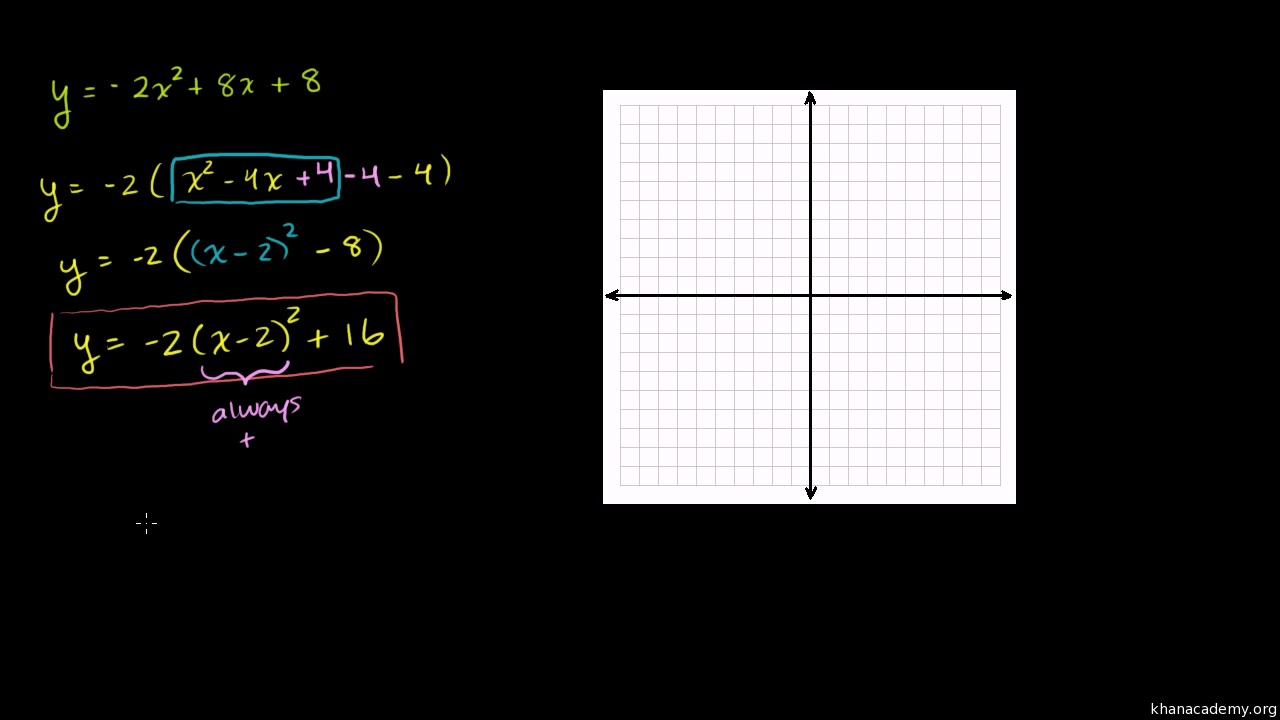
Qudratic y = x2 4x — 3 to vertex form Step 1 Find the value of b then divide it by two, First find the value of "b " b = 4 Then, divide b by two Step 2 Square it or (—)2 (2)2 = Step 3 Add and subtract that value Now that the trinomial is a perfect square, write itQuestion Rewrite the equation y=–2x^24x3 in vertex form Identify the vertex and the axis of symmetry Answer by ewatrrr(243) (Show Source) You can put this solution on YOUR website! Convert to vertex form ( y = a (x b)^2 c where (b, c) is the vertex ) y = x^2 4x y = (x 2)^2 4 so the vertex is at ( 2, 4) answer

Ppt Warm Up 2 25 13 Find The Axis Of Symmetry 1 Y 4 X 2 7 2 Y X 2 3 X 1 3 Y 2 X 2 4 X Powerpoint Presentation Id

How Do You Graph Y 2x 2 4x 3 Mathskey Com

 The equation of a parabola in vertex form is y = a(x h)² k where (h, k) are the coordinates of the vertex and a is a multiplier To obtain this form use the method of completing the square add/ subtract (half the coefficient of the x term )² y = x² 4x (2)² (2)² 11 = x² 4x 4 4 11 = (x 2)² 7 ← in vertex form4 x 2 8 x 8 = y Subtract y from both sides Subtract y from both sides 4x^ {2}8x8y=0 4 x 2 8 x 8 − y = 0 This equation is in standard form ax^ {2}bxc=0 Substitute 4 for a, 8 for b, and 8y for c in the quadratic formula, \frac {b±\sqrt {b^ {2}4ac}} {2a}Find the Vertex y=x^24x3 Rewrite the equation in vertex form Tap for more steps Complete the square for Tap for more steps Use the form , to find the values of , , and Consider the vertex form of a parabola Substitute the values of and into the formula Find the vertex

Solution Graph F X X 2 4x 3 Labeling The Y Intercept Vertex And Axis Of Symmetry Please Help

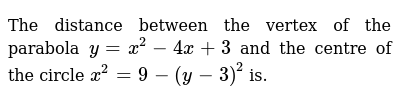
The Distance Between The Vertex Of The Parabola Y X 2 4x 3 And The Centre Of The Circle X 2 9 Y 3 2 Is

Sketch the graph, find the vertex, the focus, and the directrix Parabola The conic with the value of eccentricity standing as unity is the curve called theWe are given the function {eq}y=5x^24x3 {/eq} We want to know the vertex of the given function So, we have Solution The graph of the givenAnswer (1 of 4) The coordinates of the vertex are (2,1) Solution The function is a quadratic function that is written in standard form, ax^2 bx c = 0, a not 0 Rewrite the function in vertex form, a(x h)^2 k, a not 0 by completing the square on the original function The coordinates

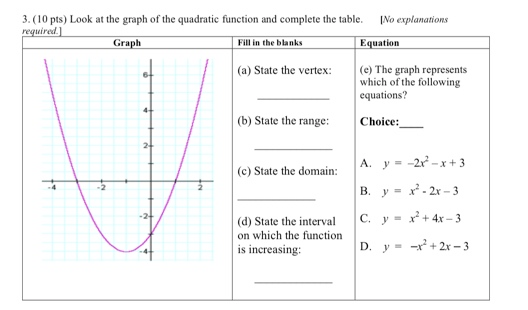
Solved 3 10 Pts Look At The Graph Of The Quadratic Chegg Com

Manhassetschools Org

F(x)= x^24x3 to find the vertex, use (b/2a) 4/2(1) = 4/2 = 2 This is the x part of the vertex (2,?), then we use 2 in place of x in f(x) f(2) = (2)^24(2)3 = 4 = 1 Therefore the vertex is (2,1) To find the x intercepts, you set the equation to equal 0 x^24x3=0 (does it factor?) (x3)=0, (x1)=0 x= 3, x=1 To find the yAnswer Vertex form of quadratic equation is => Y = a(X h)^2 k Let's simplify the given equation Add and subtract coefficient of X^2 on left side Y = 4X^2 8X 4 4 3 => Y = 4(X^2 2X 1) 4 3 => Y = 4(X 1)^2 1 So vertex of this parabola is V = (1,1)Correct answers 3 question Write y = x2 − 4x − 1 in vertex form y = (x 2)2 − 5 y = (x 2)2 5 y = (x − 2)2 − 5 y = (x − 2)2 5

Vertex Axis Of Symmetry Of A Parabola Video Khan Academy

What Is The Vertex Of Y 2x 2 4x 12 Socratic

Vertex f (x)=y=x^24x \square!Functionvertexcalculator vertex f(x)=x^{2} en Related Symbolab blog posts Functions A function basically relates an input to an output, there's an input, aGiven y= 8x^2 4x 3 We need to find the vertex We know that a= 8 b= 4 c = 3 Let V be the vertex such that V (xv, yv) xv = b/ 2a ==> 4/2*8 = 4/16 = 1/4

Vertex Axis Of Symmetry Of A Parabola Video Khan Academy

How Do You Write F X X 2 4x In Vertex Form Socratic

Transcribed image text Question 14 of 50 Find the coordinate of the vertex of the parabola y = x^2 4x 1 by making use of maxima and minima since the vertex of the parabola could be the minimum or maximum point Select the correct response (2,3) (21) (12) (3,2) Question 22 of 50 What is the area bounded by the curve y = 6 cos x and the xaxis from x pi/6 to x = pi/2?Algebra > Trigonometrybasics> SOLUTION how do you identify the vertex, focus, and directrix of the parabola y=x^24x3 And graph it Log On Algebra Trigonometry SectionAlgebra > Graphs> SOLUTION graph f(x)=x^24x3, labeling the yintercept, vertex, and axis of symmetry please help Log On Algebra Graphs, graphing equations and inequalities Section

Tutor Fur Schuler Solutions To Exercises On Vertex

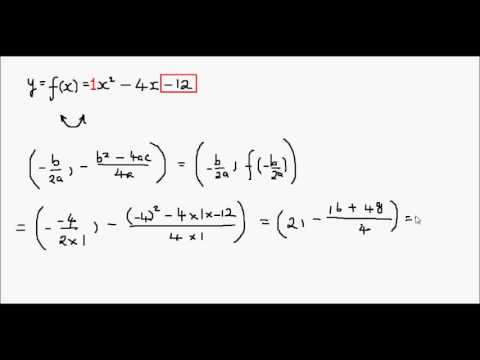
How To Sketch A Parabola Example 2 Y X 2 4x 12 Youtube

View this answer The given equation is y =x24x−3 y = x 2 4 x − 3 To convert this into the vertex form, we have to complete the squares Adding 3 3 on both sides

Undefined College Algebra Openstax Cnx

Ocr Mei Core 1 3 04 Sketch The Graph Of Y X 2 4x 4 Youtube

How Do You Graph Y 2x 2 4x 3 Mathskey Com

How To Draw Y 2 X 2 Interactive Mathematics

Scasd Org

How Do You Find The Vertex Of F X 2x 2 4x 6 Socratic

Graphing Quadratic Functions

Tatecountyschools Org

Solution Solve By Vertex Form Y X 2 6x 12 Y 4x 2 24x 11

Content Transformations Of The Parabola

Why Is It In Vertex Form Of Quadratic Function Y A X H 2 K Getting Value Of H Is Opposite To Its Value Quora

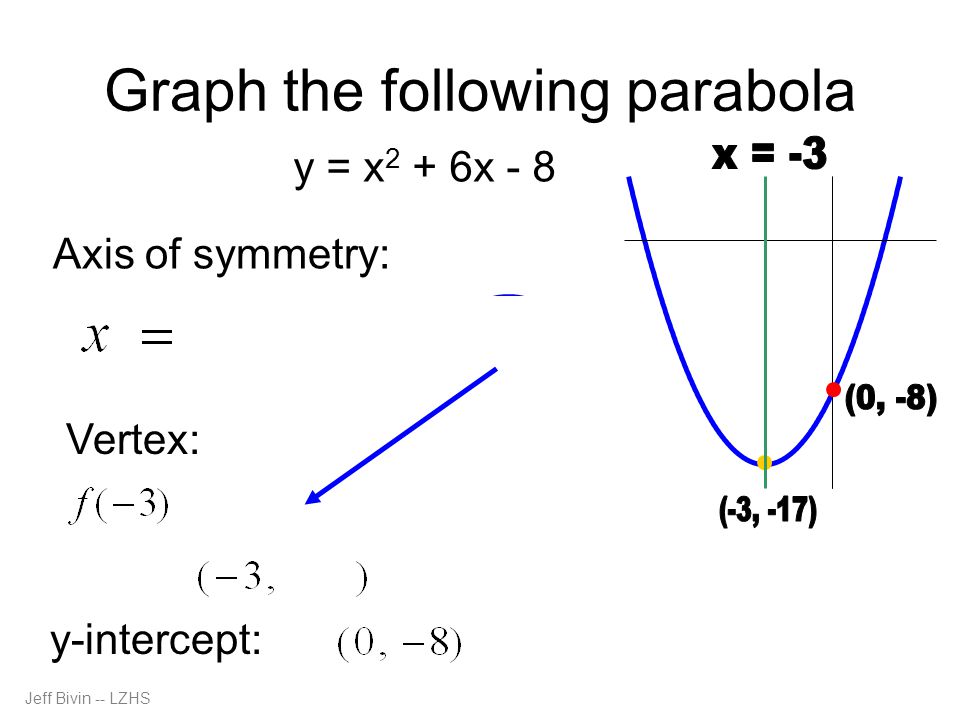
Graphing Parabolas Using The Vertex Axis Of Symmetry Y Intercept By Jeffrey Bivin Lake Zurich High School Last Updated October Ppt Download

1

What Are The Coordinates Of The Vertex For F X X 4x 10 Quora

5 3 Vertex Form Of Quadratic Functions Translating

What Is The Vertex Of Y X 2 4x 1 Socratic

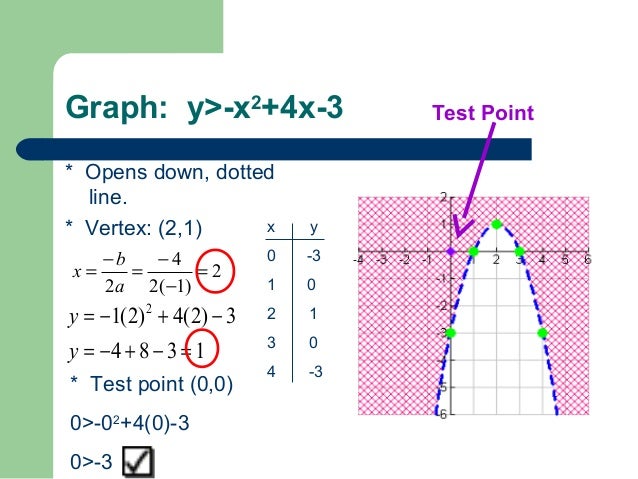
5 8 Graphing Quadratic Inequalities

Learn How To Convert To Vertex Form By Completing The Square And Then Graph Y X 2 4x 7 Youtube

Graph The Equation Y X 2 4x 3 On The Accompanying Set Of Axes You Must Plot 5 Points Including The Roots And The Vertex Using The Graph Determine The Roots Of The Equation X 2 4x 3 0

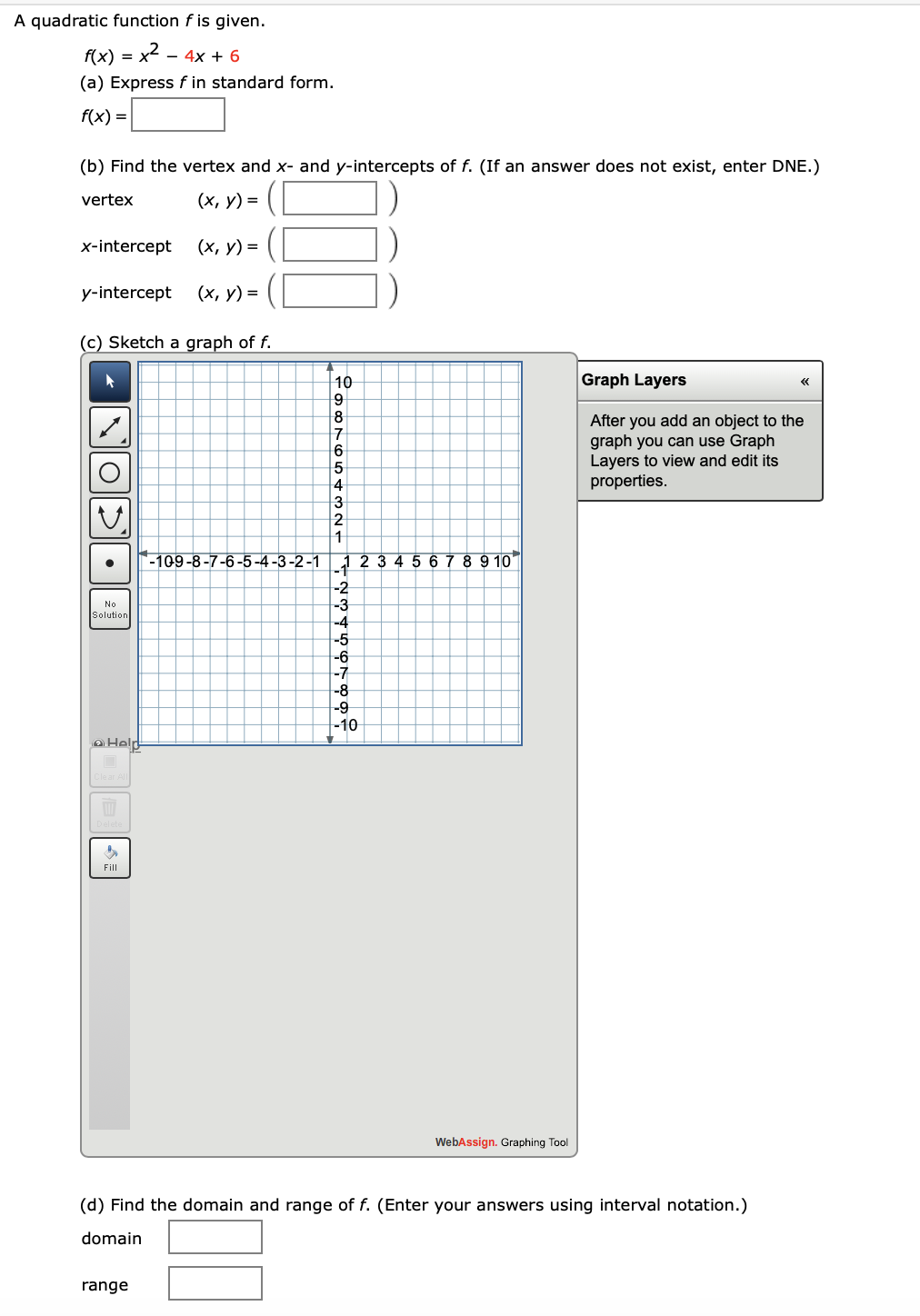
Answered A Quadratic Function F Is Given F X Bartleby

Step To Draw Y X 2 4x 1and Find Solution To Quadratic Equation Y X 2 5x 4 Youtube

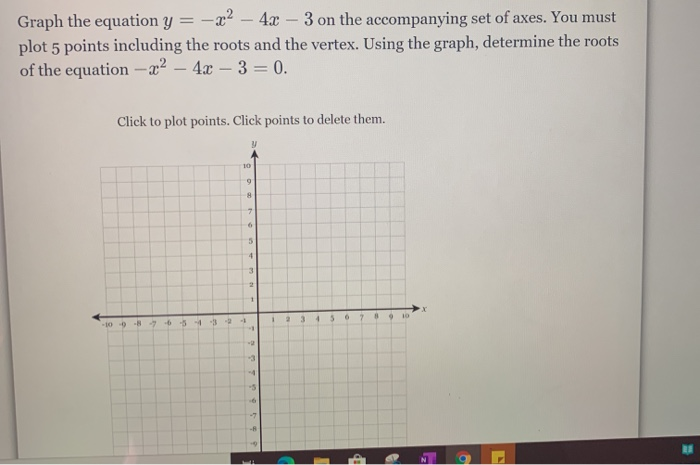
Solved Graph The Equation Y X2 4x 3 On The Chegg Com

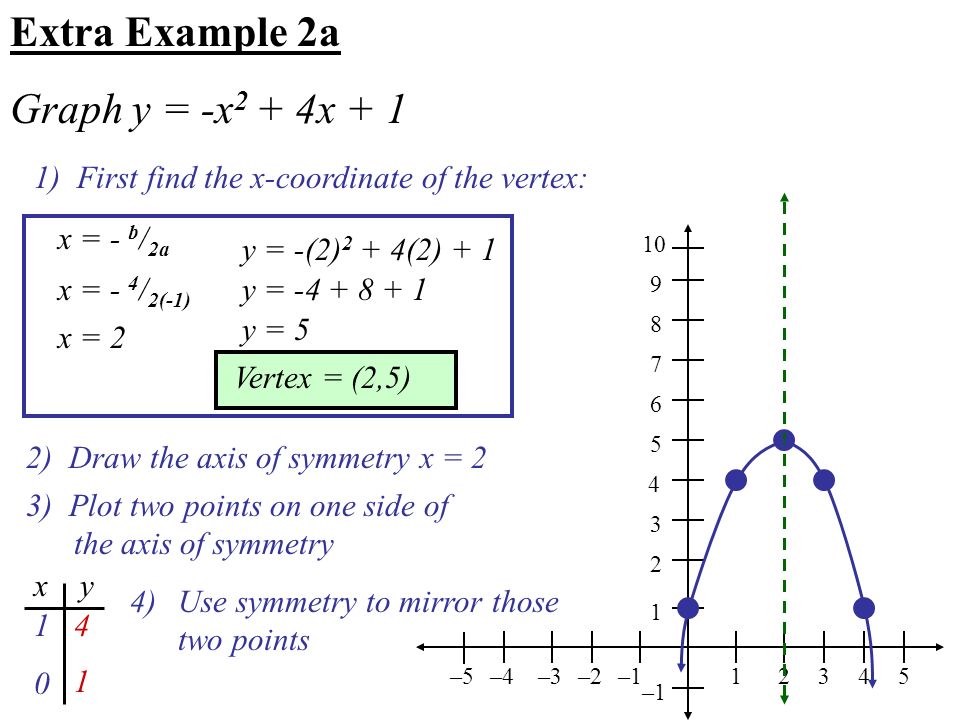
Ch 5 Notes Ppt Video Online Download

What Is The Vertex Of Y X 4x 5 Quora

Pshs Psd2 Org

Solution Use A Table To Graph They Function Y X 2 4 3 Ho Do U Graph It Including The Parabolas And Axis Of Symetry And The Vertex As A Maximum Or Minumum

Practice 10 2 Quadratic Functions

Y X2 4x 6 Math Homework Answers

Exploration Of Parabolas

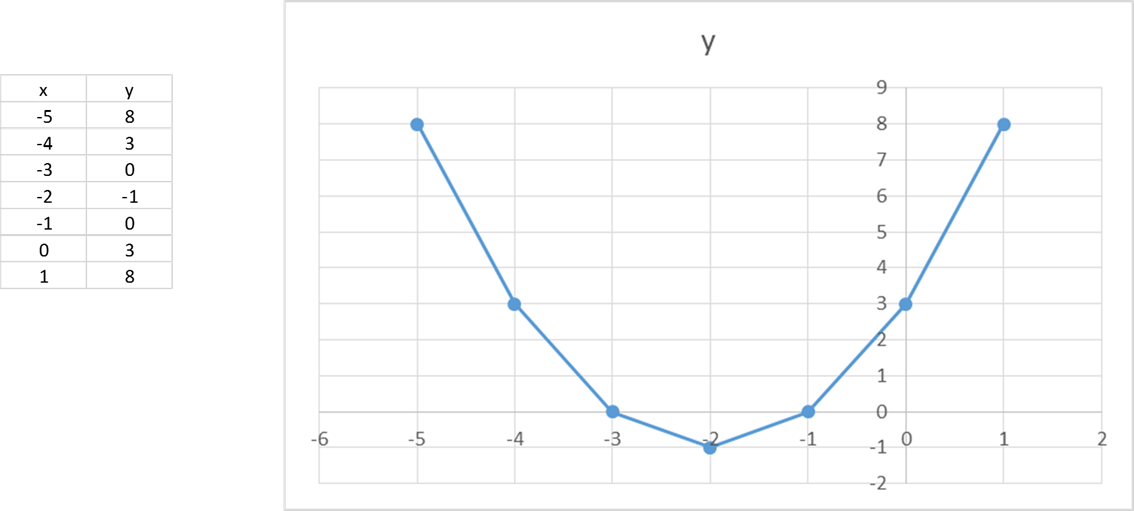
How Do You Graph Y X 2 4x 3 Socratic

Plot A Graph For The Equation Y X 2 4x 1

Lessons 5

The Vertex Form Of The Function Is Choose The Equation That Shows A Step In The Process Of Brainly Com

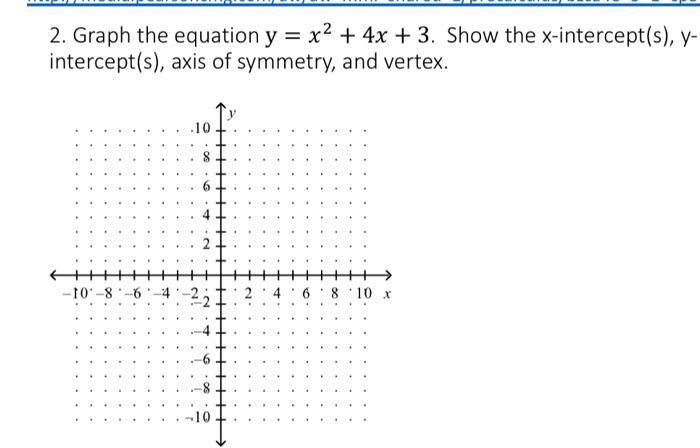
Solved 2 Graph The Equation Y X2 4x 3 Show The Chegg Com

17 03 02consider The Basic Quadratic Function F X Qudratic Y X2 4x 3 To Vertex Form Step 1 Y 8x F Y X 2 9x 2 Xo Qx A Pdf Document

How To Find The Vertex Of A Quadratic Equation 10 Steps

Given Function F X X2 4x 5 Determine The Vertex Axis Of Symmetry Calculate Y Intercept Find Additional Point On Graph Graph Function Submit Graph Enotes Com

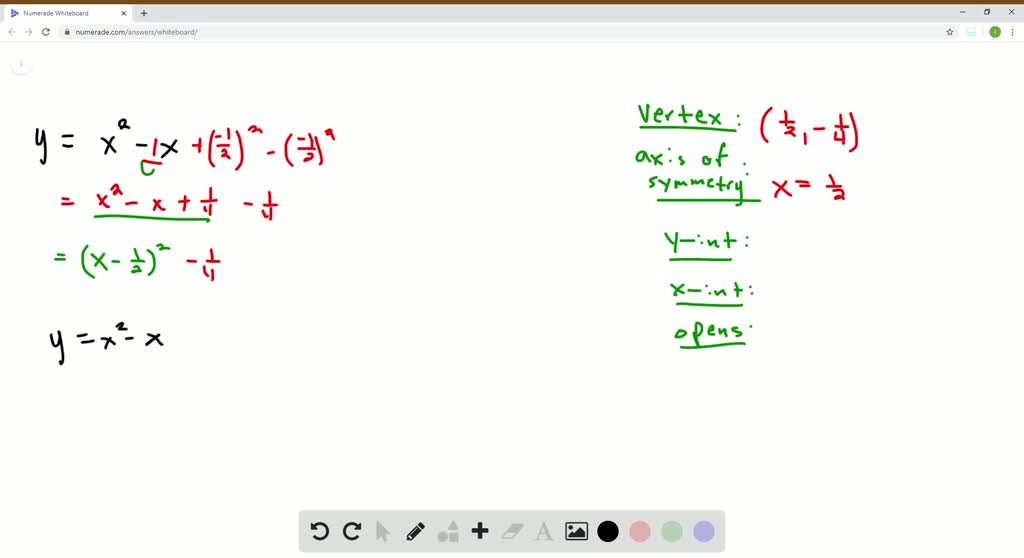
Solved Quadratic Equations Graph The Equation Y X2 4x 3 Show The X Intercept S Y Intercept S Axis Of Symmetry And Vertex Show Your Work For Each Part And Explain Your Steps As If You Were Teaching The Process

How Do You Graph Quadratic Functions Y X 2 4x 7 Socratic

Which Of The Following Quadratic Functions Has A G Gauthmath

Solution Y X2 4x 3 Of This Equation What Is The Line Of Symmetry The Vertex

Solution Graph Y X2 4x 7 And Determine The Maximum Or Minimum The Vertex And The Axis Of Symmetry

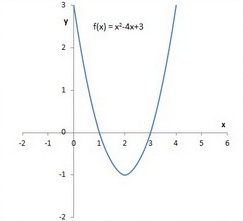
How Do I Convert The Equation F X X 2 4x 3 To Vertex Form Socratic

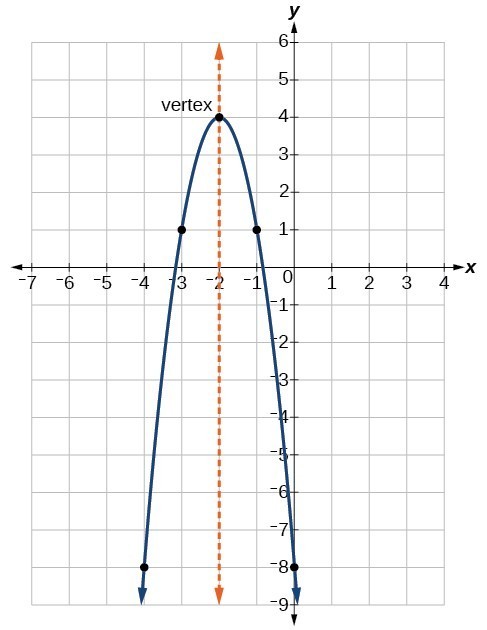
Understand How The Graph Of A Parabola Is Related To Its Quadratic Function College Algebra

Identify The Vertex Of The Parabola Y X2 4x 3 Brainly Ph

Quadratics Graphing Parabolas Sparknotes

Ch 5 Notes Ppt Video Online Download

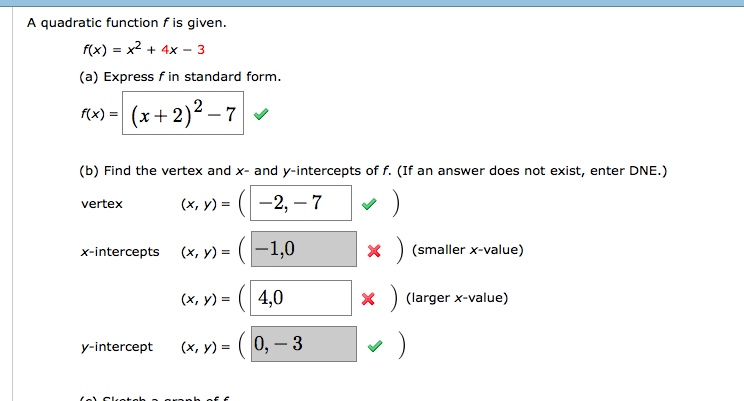
Solved A Quadratic Function F Is Given F X X2 4x 3 A Chegg Com

Answered Find The Vertex Y Intercept And X Bartleby

Example 6 Write A Quadratic Function In Vertex

1 Find The Vertex Point H K 2 A Will Be The A From The Standard Form Equation 3 Substitute Into Y A X H 2 K Ppt Download

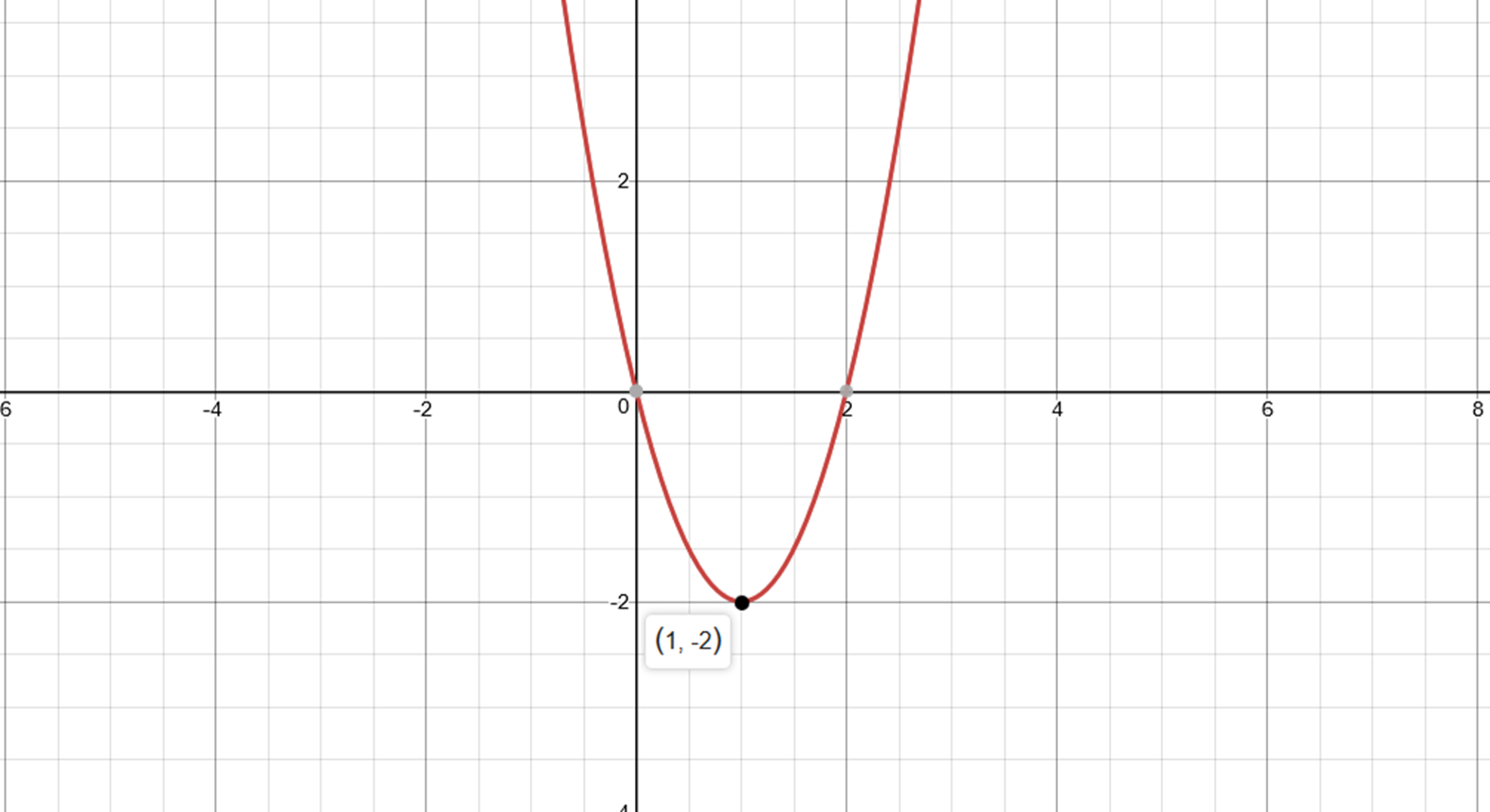
The Graph Of Y X 2 4x 3 Is Shown What Are The Coordinates Of The Turning Point

What Is The The Vertex Of Y X 2 4x Socratic

Help 6 6 Given The Equation Y X2 4x 3 A 3 Pts Homeworklib

5 3 The Graphs Of Quadratic Equations X

Graph The Equation Y X2 4x 3 On The Accompanying S Gauthmath

3 Vertex Form

3 2 Quadratic Functions Mathematics Libretexts

What Are The Vertex And X Intercepts Of The Graph Of Y X2 4x 21 Select One Answer For The Vertex Brainly Com

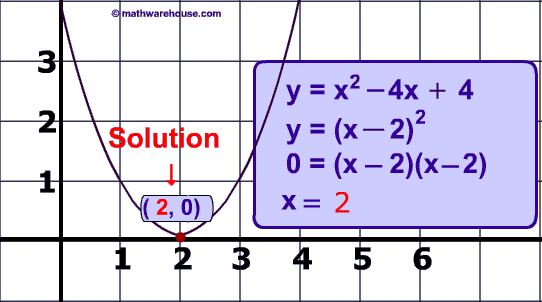
How To Solve Quadratic Equation By Factoring Video Tutorial Practice Problems Plus Worksheet With Answer Key

A Quadratic Function F Is Given Flx X2 4x 3 A Express F In Transformation Homeworklib

Characteristics Of Parabolas College Algebra

1

Lcps Org

Quadratic Function

Y Classzone

Graph The Parabola Y X 2 4x 1 Youtube

The Distance Between The Vertex Of The Parabola Y X 2 4x 3 And The Centre Of The Circle X 2 9 Y 3 2 Is

Solution Graph F X X 2 4x 3 Labeling The Y Intercept Vertex And Axis Of Symmetry

Example 6 Write A Quadratic Function In Vertex Form Write Y X 2 10x 22 In Vertex Form Then Identify The Vertex Y X 2 10x 22 Write Original Ppt Download

Solved 5 Write The Equation Of The Parabola In Vertex Form Chegg Com

2 02 Quadratic Equations

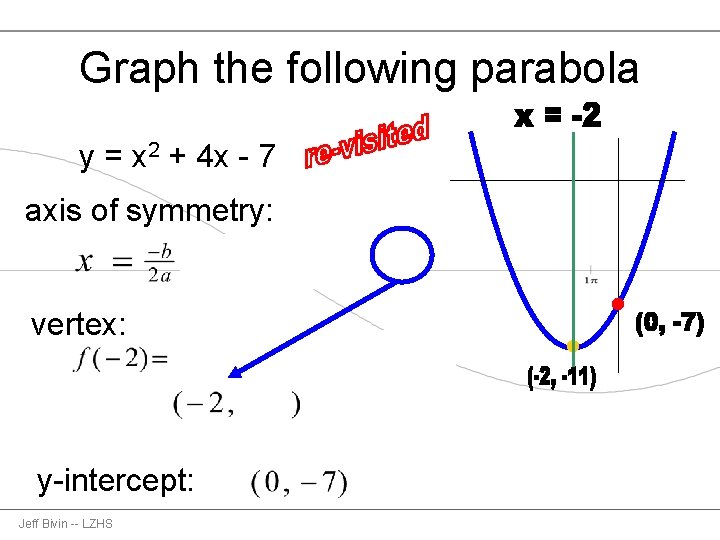
Graphing Parabolas Using The Vertex Axis Of Symmetry

17 03 02consider The Basic Quadratic Function F X Qudratic Y X2 4x 3 To Vertex Form Step 1 Y 8x F Y X 2 9x 2 Xo Qx A Pdf Document

1

Unique Quadratic Equation In The Form Y Ax 2 Bx C

Olma Org

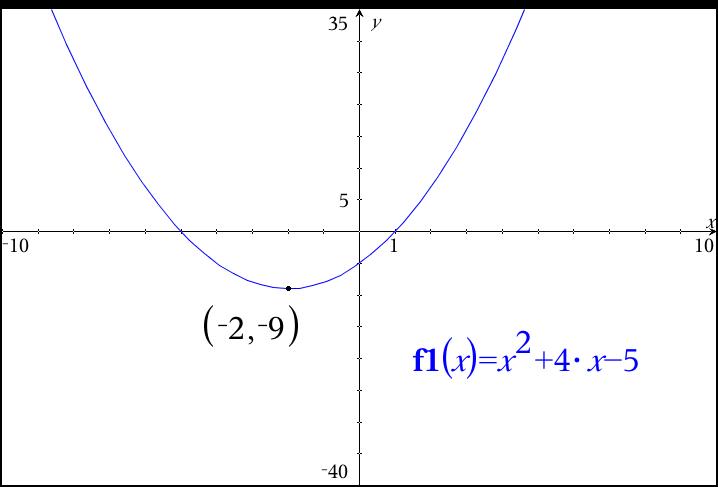
What Is The Vertex Of F X X 2 4x 5 Socratic